一、最短路径的定义

对在有权图 $G=(V,E)$ ，从一个源点s到汇点t有很多条路径，其中路径上权值和最小的路径，称从s到t的最短路径。

简单讲：找出连接两个给定顶点权值和最小的路径。

二、最短路径问题的分类及算法

SSSP：求给定起点S到其他所有点的最短路，常见算法有Dijkstra算法、Bellman_Ford算法及SPFA算法；
APSP：求任意两对顶点之间的最短路，常见算法有Floyd算法；

这两种情况在做题时一定要分清

（一）Floyd算法（APSP）

算法概述

Floyd算法借助DP思想，可以求出每对点之间的最短距离，它对于图的要求是，可以是无向图和有向图，边权可正可负，唯一的要求是不能有负环。

算法原理

定义 $d[i][j][k]$ 为路径中间只允许经过节点 $1...k$ 的情况下，i到j的最短路距离。

它有两种情况：

最短路经过点k， $d[i][j][k]=d[i][k][k-1]+d[k][j][k-1]$
最短路不经过点k， $d[i][j][k]=d[i][j][k-1]$

综合起来，状态转移方程为：

$d[i][j][k]=min\left\{d[i][k][k-1]+d[k][j][k-1],d[i][j][k-1] \right\}$

边界条件： $d[i][j][0]=len[i][j]$ （不存在的边权可为∞）相信大家已经看出来，我们实际上只是做了一次动态规划。由于在递推过程中k是递增的，所以我们只需要一个二维数组就可以了。

具体来说就是：初始 $d[i][j]=w[i][j]$ 。从小到大枚举k，对每对结点 $(u,v)$ ，检查更新它们的最短路值。

核心代码

非常简单粗暴，时间复杂度： $O(n^3)$

for(k=1;k<=n;k++) //枚举中间点
    for(i=1;i<=n;i++) //枚举起点
        for(j=1;j<=n;j++) //枚举终点
            if((d[i][k]!=INF)&&(d[k][j]!=INF)&&(d[i][k]+d[k][j]<d[i][j])) 
                d[i][j]=d[i][k]+d[k][j];

该算法例题

1624 -- 【模拟试题】图的直径

Description

图的直径是这样定义的：在一个带正权的图中，它的直径是指任意两点之间最短路的最大距离。注意：此图为无向图。
Input

第一行有两个正整数N,M,分别表示点数和边数(N<=100,M<=10000）。
接下来M行，每行三个正整数，分别表示每一条边的两个端点编号和长度。
　　
Output

输出只有一行为这个图的直径。
　　
Sample Input

3 3
1 2 1
2 3 2
1 3 2

Sample Output

2

这显然是APSP，即任意两对顶点之间的最短路

代码实现：

初始化 $d[i][j]=\begin{cases}0&i=j\\∞&i\ne j\end{cases}$
读入数据
跑一遍Floyd
枚举结点 $i$ 和点 $j$ ，找到 $d[i][j]$ 的最大值并输出

由于上面已经说的很清楚了，所以代码里面没有太多注释

#include<iostream>
#include<cstdio>
#define maxn 5003
#define yao_bu_ke_ji 0x3f3f3f3f
using namespace std;
int n,m;
int fd[maxn][maxn];

int floyed() {
	for(int mid=1; mid<=n; mid++) {
		for(int i=1; i<=n; i++) {
			for(int j=1; j<=n; j++) {
				if(fd[i][mid]<yao_bu_ke_ji-5&&fd[mid][j]<yao_bu_ke_ji-5) {
					fd[i][j]=min(fd[i][j],fd[i][mid]+fd[mid][j]);
				}
			}
		}
	}
}
int main() {
	cin>>n>>m;
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) {
			if(i==j) fd[i][j]=0;
			else fd[i][j]=yao_bu_ke_ji;
			
		}
	}
	for(int i=1; i<=m; i++) {
		int x,y;
		cin>>x>>y;
		cin>>fd[x][y];//cin要 分开写！ 分开写！ 分开写！
		fd[y][x]=fd[x][y]; 
	}
	floyed();
	int ans=-yao_bu_ke_ji;
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) {
			if(fd[i][j]<yao_bu_ke_ji-3) ans=max(ans,fd[i][j]);
			
		}
	}
	cout<<ans<<endl;
	return 0;
}

选址类问题

现准备在n个居民点v1,v2,...,vn中设置一银行，问设在哪个点，可使最大服务距离最小？
若设置两个银行，问设在哪两个点?

假设各个居民点都有条件设置银行，并有路相连，且路长已知。实质就是求图的中心问题。

设置一个银行的情况：

初始化 $d[i][j]=\begin{cases}0&i=j\\∞&i\ne j\end{cases}$
读入数据，邻接矩阵存储；
用Floyd求任意两点间的最短距离 $d[i][j]$ ；
枚举点 $i$ ，找到其它点的最短路径的最大值，即 $t[i]=max \left\{t[i],d[i][j]\right\}(1\le j\le n)$
$ans=min \left\{ans,t[i]\right\}(1\le i\le n)$

#include<iostream>
#include<cstdio>
#define maxn 6120
#define sky 0x7fffffff/2
using namespace std;
int n,m;
int fd[maxn][maxn];
void floyed() {
   	for(int mid=1; mid<=n; mid++) {
   		for(int i=1; i<=n; i++) {
   			for(int j=1; j<=n; j++) {
   				if(fd[i][mid]<sky-3&&fd[mid][j]<sky-3) {
   					fd[i][j]=min(fd[i][j],fd[i][mid]+fd[mid][j]);
   				}
   			}
   		}
   	}
}
int main() {
   	cin>>n;
   	m=n-1;
   	for(int i=1; i<=n; i++) {
   		for(int j=1; j<=n; j++) {
   			if(i==j) fd[i][j]=0;
   			else fd[i][j]=sky;
   		} 
   	}
   	for(int i=1; i<=m; i++) {
   		int x,y;
   		cin>>x>>y;
   		cin>>fd[x][y];
   		fd[y][x]=fd[x][y];
   	}
   	
   	floyed();
   	int anss[maxn];
   	for(int i=1; i<=n; i++) {
   		int ans=-sky;
   		for(int j=1; j<=n; j++) {
   			if(fd[i][j]<sky-3) ans=max(ans,fd[i][j]);
   		}
   		anss[i]=ans;
   	}
   	int reans=sky,aans;
   	for(int i=1; i<=n; i++) {
   //		reans=min(anss[i],reans);
   		if(anss[i]<reans) {
   			reans=anss[i];
   			aans=i;
   		}
   	}
   	cout<<aans;
	return 0;
}

设置两个银行的情况
1. 初始化 $d[i][j]=\begin{cases}0&i=j\\∞&i\ne j\end{cases}$
2. 读入数据，邻接矩阵存储；
3. 设两个银行设置在点 $i$ 和点 $j$ ,枚举 $k$ （居民点），求出到 $j$ 距离的最小值，再找出所有 $k$ 中最大值，即为在 $i,j$ 设置银行的最大服务距离： $t[i][j]=max \left\{t[i][j],min(d[i][k],d[j][k])(1\le k \le n)\right\}(1\le i<j\le n)$
4. $ans=min \left\{ans,t[i][j]\right\}(1\le i<j\le n)$
~~代码走丢了~~

（二）Dijkstra算法（SSSP）

算法思想

如果图是不带负权的有向图或者无向图，我们可以用类似Prim算法的贪心思想，从起点 $v0$ 每次新扩展一个距离最短的点，再以这个点为中间点，更新起点到其他所有点的距离。由于所有边权都为正，故不会存在一个距离更短的没被扩展过的点，所以这个点的距离永远不会再被改变，因而保证了算法的正确性。

算法实现时，用一维数组 $vst[i]$ 表示源点到顶点i的最短距离求出没有。用 $d[i]$ 记录源点 $v0$ 到顶点 $i$ 的距离值。

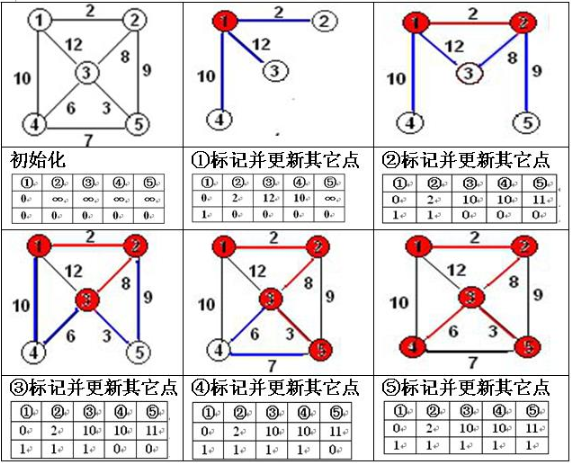
算法步骤

初始化 $d[v0]=0$ ，源点到其它点的距离值 $d[i]=∞$ ；
经过 $n$ 次如下步骤操作，最后得到 $v0$ 到 $n$ 个顶点的最短距离；

A. 选择一个未标记的点 $k$ 并且 $d[k]$ 的值是最小的；

B. 标记点 $k$ ，即 $vst[k]=1$ ；

C. 以 $k$ 为中间点，修改源点 $v0$ 到其他未标记点 $j$ 的距离值 $d[j]$

【图论算法】最短路径