$Part0$ —— DP入门思想

首先，我们来一道极其水沝淼㵘的入门思考题：

【题目简述】给出你一个地图，地图中每个顶点代表一个城市，两个城市间的连线代表道路，连线上的数值代表道路的长度。现在，想从城市A到达城市D，怎样走路程最短，最短路程的长度是多少？

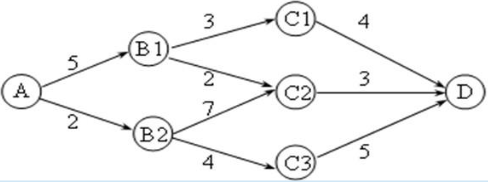
看完题后，我们发现这里共有 $4$ 条路径：

而怎么找最短路径呢？

【方法1】如果采用枚举算法，分别枚举出4条路径，然后比较每条路经的长度，得出最优解10，路径为A→B1→C2→D。

【方法2】如果我们采用分层递推的思想来做这个题目，会出现什么结果呢？设F(i)表示从点A到达点i的最短距离，则有：

$F(A)=0$

$F(B1)=min\left\{F(A)+5\right\}=5$

$F(B2)=min\left\{F(A)+2\right\}=2$

$F(C1)=min\left\{F(B1)+3\right\}=8$

$F(C2)=min\left\{F(B1)+2,F(B2)+7\right\}=7$

$F(C3)=min\left\{F(B2)+4\right\}=6$

$F(D)=min\left\{F(C1)+4,F(C2)+3,F(C3)+5\right\}=10$

所以从A到D的最短距离是10，路径为A→B1→C2→D。